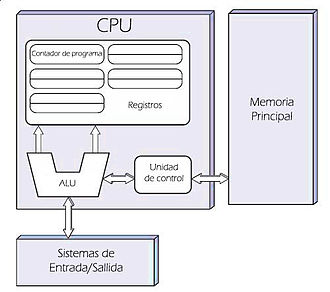
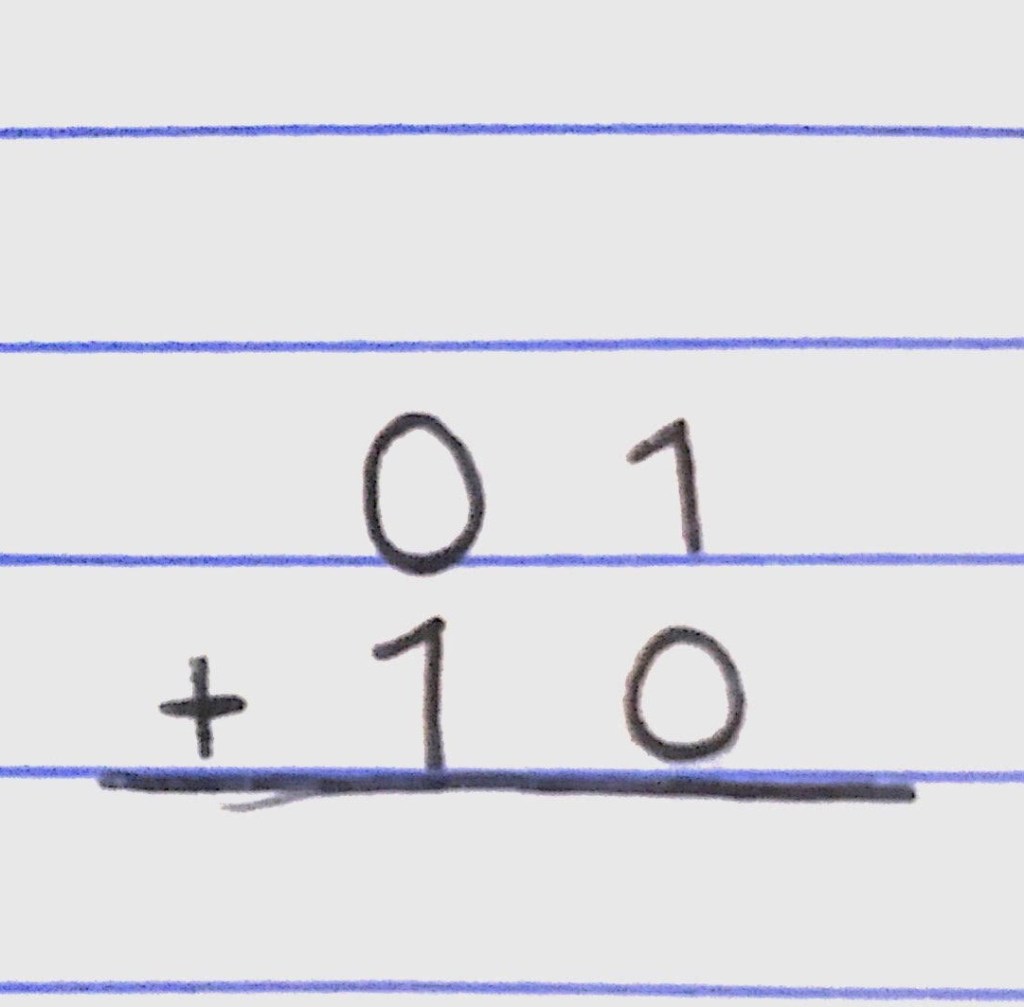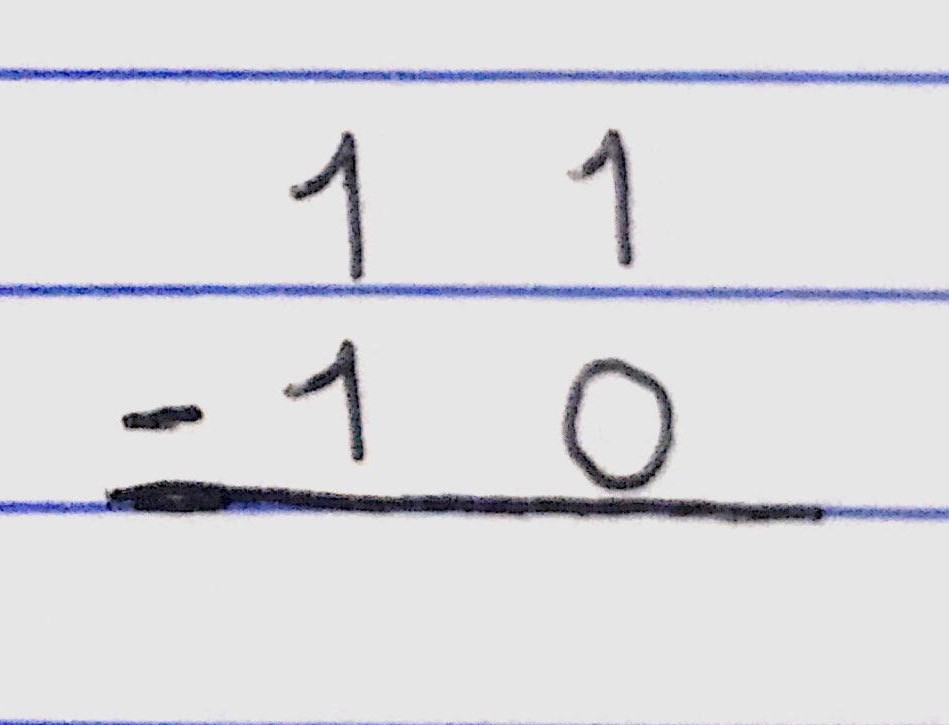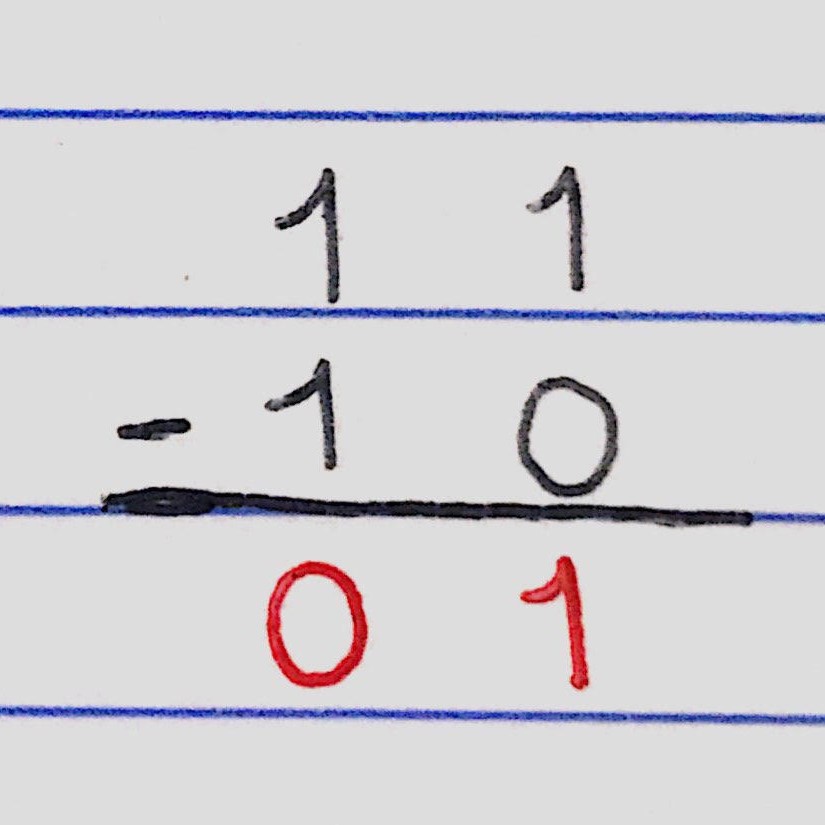A continuación veremos los términos, conversiones, operaciones matemáticas en sistemas numéricos y descubriremos ¿Que es «Bitwise Operators»?

En una computadora uno es capaz de almacenar varios trabajos u documentos que constan de diferentes tamaños que ocupan en el espacio de una memoria. Todos estos datos son grabados en las computadoras en forma de bits; para que la máquina pueda acceder a los datos y comprender lo que esta en bits esta debe de codificarla en datos numéricos.

Un sistema numérico computacional es una serie de símbolos y reglas encargadas de la construcción de números válidos, las características de estos sistemas varían dependiendo del sistema a analizar. Básicamente los sistemas se diferencian por el número de símbolos permitidos, por ejemplo, el sistema binario consta de dos dígitos, el cero y el uno; el octal consta de ocho dígitos; el decimal de diez dígitos; y el hexadecimal de dieciséis dígitos. En el lenguaje computacional el sistema binario es el más adecuado debido a que trabajan internamente con dos niveles de voltaje, encendido y apagado, 0: apagado y 1: =encendido.

Números Binarios

Son los números que conforman al sistema numérico binario y que está constituido por solamente dos cifras: 1 y 0. Sistema en el cual se escriben cantidades, códigos, mensajes y otros lenguajes con tan solo dos elementos dentro de la numeración, haciendo que el código se simplifique la comprensión de los sistemas informáticos, pues hará que un elemento tenga un valor unitario o nulo.

Un número binario puede ser representado por cualquier secuencia de bits. Un bit es un dato que puede tener dos valores, ya sea uno o cero, por lo tanto, con un bit podemos representar solamente dos valores, si queremos representar o codificar más información en un dispositivo digital, necesitamos una mayor cantidad de bits. Si usamos dos bits, tendremos cuatro combinaciones posibles, si usamos tres bits tendremos ocho posibles combinaciones, etc. En general se puede representar hasta 2n2n valores diferentes donde nn es el número de bits necesarios.

Números Octales

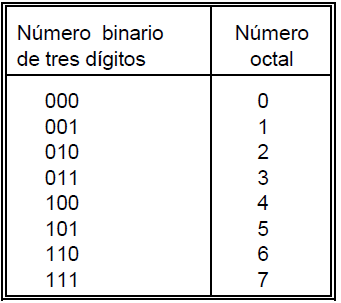
Los números octales son un sistema de numeración el cual consta con base de 8, una base que es potencia exacta de 2 o de la numeración binaria. Se le llama octal ya que los dígitos que se encontrarán en un octal serán del 0-7 (0, 1, 2, 3, 4, 5, 6, 7). Usualmente se utiliza más el sistema octal que el hexadecimal ya que no requiere de utilizar otros símbolo como letras como el hexadecimal, el cual requiere de ellos. Sin embargo, para trabajar con bytes o conjuntos de ellos, asumiendo de que el byte sera una palabra de 8 bits, suele ser mas cómodo utilizar el sistema hexadecimal.

En la tabla, se muestra el equivalente de cada número octal en número binario, siendo estos un conjunto de 3 cifras de 0 y 1.

Números Hexadecimales

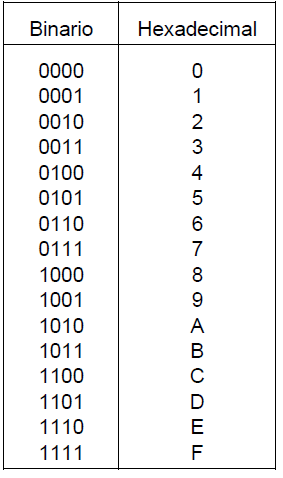
Los números hexadecimales son un sistema de numeración posicional que consta de una base de 16, siendo sus dígitos del 0-15, con la condición de que es del 0-9 y del 10-15 se reemplazaran con las primeras letras del abecedarios en orden alfabetico, siendo:
10 = A
11 = B
12 = C
13 = D
14 = E
15 = F
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)
Este sistema esta muy vinculado con las áreas de informática, sistemas y otras ciencias de la computación por el gran uso que se le da dentro de una maquina (computadora/CPU) para la conversión de bytes a datos.
Tal y como se explican en la tabla, se muestra la equivalente de un número hexadecimal en número binario, siendo en binario un dígito de 4 cifras de 0 y 1.

Operaciones Matemáticas en Sistemas Numéricos

Suma en Binarios

Para empezar hay que conocer las 4 reglas de la suma de los números binarios:
1. 0 + 0 =    0  (cero + cero = cero)
2. 0 + 1 =    1  (cero + uno = uno)
3. 1 + 0 =    1  (uno + cero = uno)
4. 1 + 1 = 1 0  (uno + uno = uno(acarreo) cero(suma)

En la última regla 4 podemos ver que hay un 1 y un 0, esto no es un 10 sino ambos números separados, siendo el 1 el acarreo y el 0 la suma. El acarreo es «llevarse una» cuando realizas una suma, tanto en el sistema binario como en cualquier otro. Vas sumando uno al dígito de la derecha y cunado llegues a máximo dígito que permite la base elegida, tienes que«ponerlo a cero» y sumarle uno al dígito que está a su izquierda.
Hagamos un ejemplo:

• 

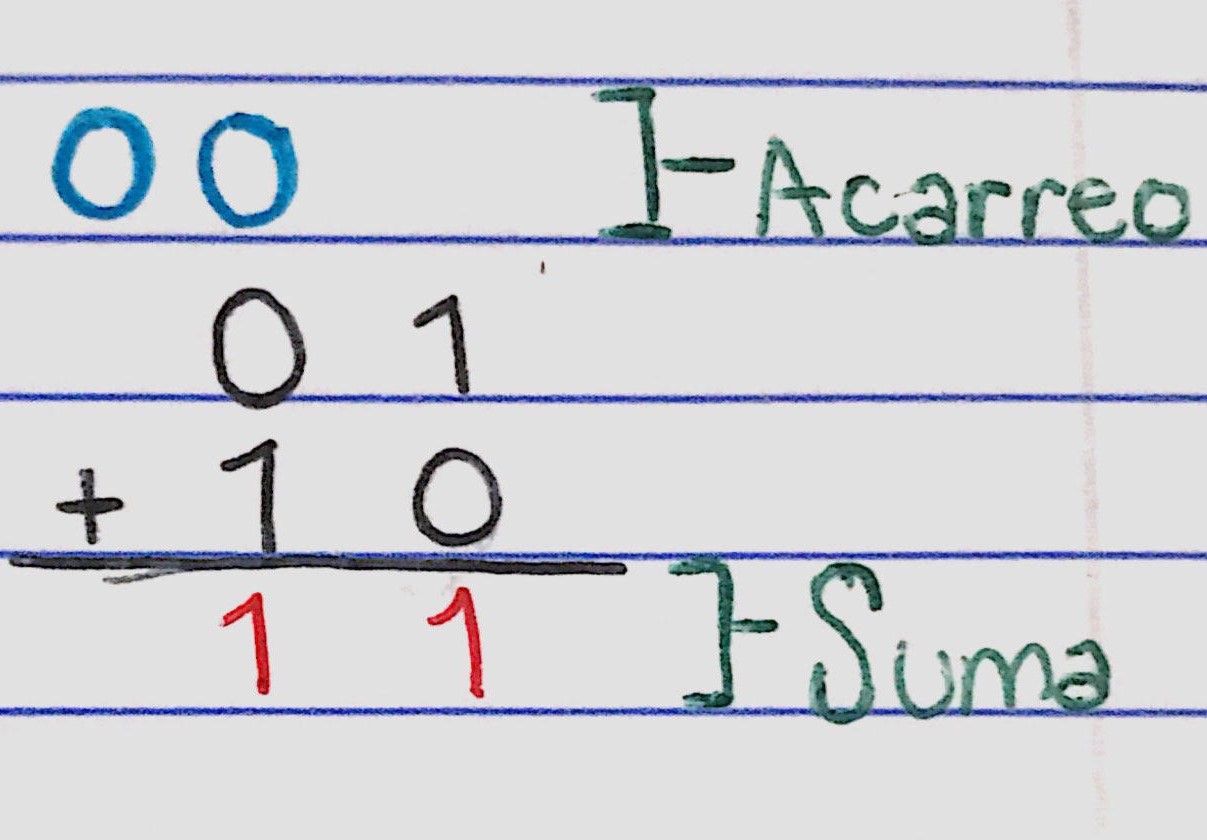
En el ejercicio tenemos 0 1 sumando a 1 0. Para empezar sumamos a los primeros de el lado derecho (como una suma normal); sumaremos usando las 4 reglas, teniendo 1 + 0 que sería su suma 1 y su acarreo 0, colocaremos al 1 como el resultado y a su acarreo lo colocaremos en la parte superior de la otra suma, para asi sumarlo con los siguientes números. Seguimos con la otra suma que sería 0 + 1, pero antes sumaremos a ese cero con el acarreo del anterior, teniendo así 0 + 0 = 0, y el resultado de este lo sumaremos con el 1, teniendo 0 + 1, el cual terminaría siendo su suma 1 y su acarreo 0, el cual pondremos en la parte superior de la siguiente suma; como vemos, ya no tenemos mas dígitos para sumar mas que el acarreo, el cual siendo cero, no lo bajamos porque no es necesario, teniendo ahora nuestro resultado de la suma de 0 1 + 1 0 = 1 1. Recordemos que en la suma de binario siempre hay que contarlos y verlos como dígitos separados.

Resta en Binarios

Como en la suma, dentro de la resta hay que conocer las 4 reglas de los números binarios:
1.      0 – 0 =  0  (cero – cero = cero)
2.  1  0 – 1 =  1  (cero – uno = uno (acarreo negativo))
3.      1 – 0 =  1  (uno – cero = uno)
4.      1 – 1 =  0  (uno – uno = cero)

Como podemos ver las reglas 1 3 y 4 son similares a las de la suma exceptuando a la segunda la cual para poder obtener el resultado 1, necesitaremos un acarreo negativo. Un acarreo negativo es pedir prestado al otro número al de la siguiente columna un dígito.
Hagamos un ejemplo:

• 

• 

Usaremos la resta de 1 1 – 1 0. Para empezar restamos desde el lado izquierdo (como una resta normal) y siguiendo las reglas, restamos 1 – 0, que según la regla 3 sería el resultado 1. Seguimos con la siguiente columna, 1 – 1, que según la regla 4 su resultado sería 0. Y ya sin quedarnos con dígitos, concluimos que:
1 1 – 1 0 = 0 1.

Representar Números Negativos

Para representar un número negativo, en las matemáticas se hace uso de un signo adicional “-” que precede al número negativo. Dado que en un sistema digital sólo se podrán disponer de los dos símbolos ya mencionados, se han ideado múltiples soluciones para representar y operar con números negativos.
Para representar número con signos existen dos razones: Signo y Magnitud, siendo el signo representando si es (+) o (-) y la magnitud el valor del número.  Partiendo de que la forma de operar en un sistema digital es a través de un conjunto definido de bits. En grupos de 8 bits (un byte), el enfoque es reservar 1 bit (normalmente el primero) para indicar el signo. Normalmente se asocia un 0 al signo “+” y un 1 al signo “-“. El resto de los bits del grupo indica la magnitud.
Así, la cifra 00000011 equivale a +3 en decimal mientras que 10000011 equivale a “-3”.

Se debe tener en cuenta los siguientes aspectos importantes:

• La magnitud absoluta que se puede representar es la mitad que si utilizáramos el grupo completo de 8 bits.  En efecto, mientras que en un grupo de 8 bits podemos almacenar desde el valor (en decimal) 0 hasta 255, si es un byte con signo podremos almacenar desde -127 hasta +127.
• A la hora de hacer operaciones debemos tratar de forma separada el signo,es decir, debemos procesar por una parte los signos y por otra las magnitudes.
• El cero está representado dos veces: 00000000 y 10000000 lo cual es poco eficiente.

Bitwise Operators

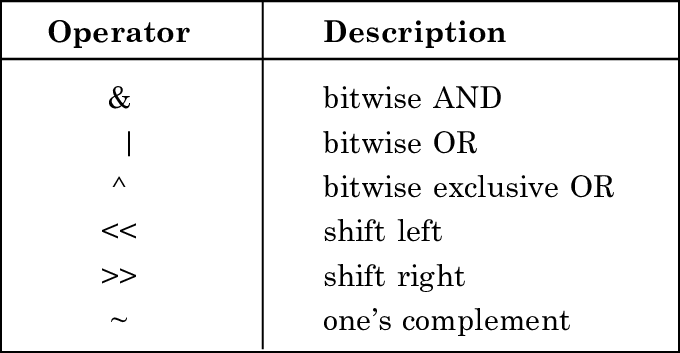
Los operadores a nivel de bit tratan sus operandos como una secuencia de 32 bits (unos y ceros) en lugar de números decimales, hexadecimales u octales.  Por ejemplo, el número decimal nueve tiene una representación binaria de 1001. Los operadores a nivel de bit realizan las operaciones en esas representaciones binarias, pero los valores devueltos son los valores numéricos estándar de JavaScript.